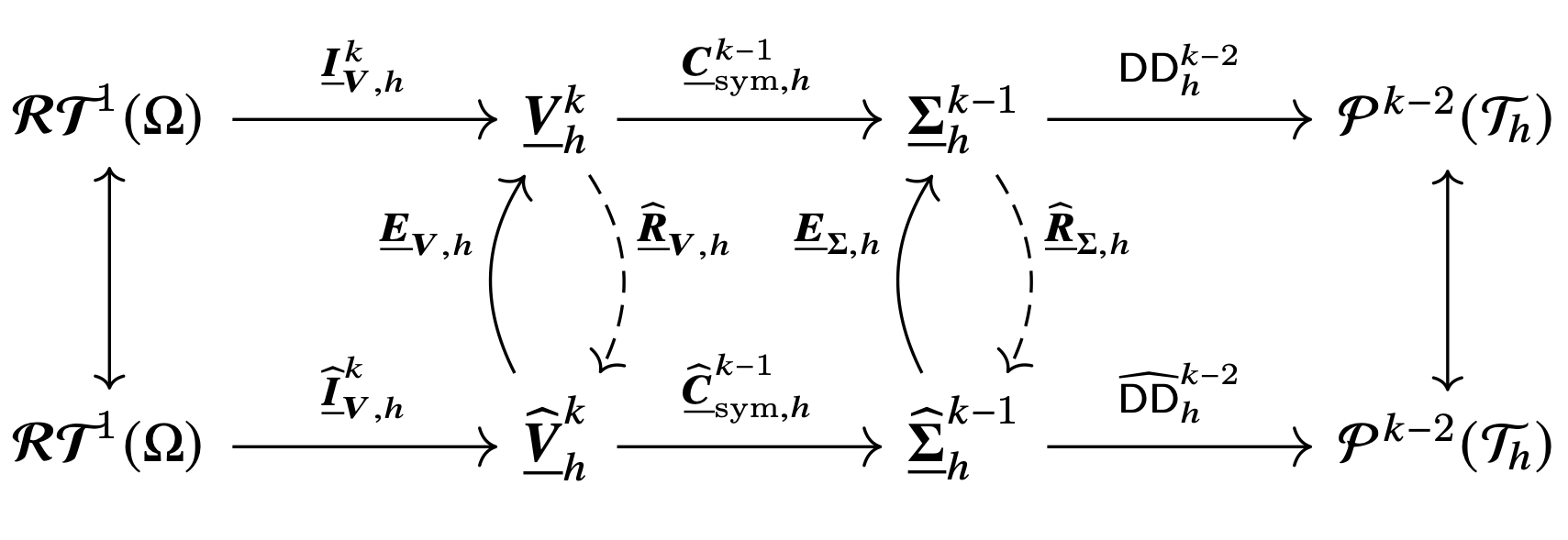
A new MOX report entitled “A serendipity fully discrete div-div complex on polygonal meshes” by Botti, M.; Di Pietro, D.A.; Salah, M. has appeared in the MOX Report Collection.
The report can be donwloaded at the following link:
https://www.mate.polimi.it/biblioteca/add/qmox/47/2022.pdf
Abstract: In this work we address the reduction of face degrees of freedom (DOFs) for discrete elasticity complexes. Specifically, using serendipity techniques, we develop a reduced version of a recently introduced two-dimensional complex arising from traces of the three-dimensional elasticity complex. The keystone of the reduction process is a new estimate of symmetric tensor-valued polynomial fields in terms of boundary values, completed with suitable projections of internal values for higher degrees. We prove an extensive set of new results for the original complex and show that the reduced complex has the same homological and analytical properties as the original one. This paper also contains an appendix with proofs of general Poincar\’e–Korn-type inequalities for hybrid fields.