A new MOX report entitled “Adaptive VEM for variable data: convergence and optimality” by Beirao da Vega, L.; Canuto, C.; Nochetto, R.H.; Vacca, G.; Verani, M. has appeared in the MOX Report Collection.
The report can be donwloaded at the following link:
https://www.mate.polimi.it/biblioteca/add/qmox/27/2023.pdf
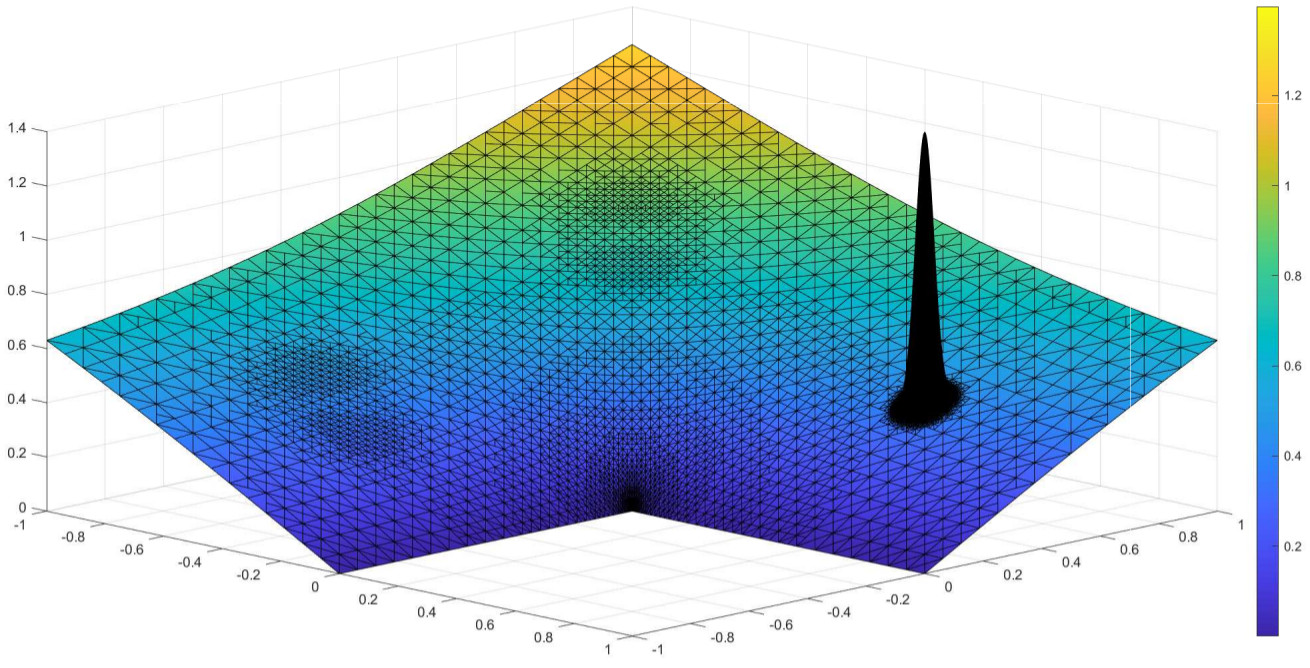
Abstract: We design an adaptive virtual element method (AVEM) of lowest order over triangular meshes with hanging nodes in 2d, which are treated as polygons. AVEM hinges on the stabilization-free a posteriori error estimators recently derived in [8]. The crucial property, that also plays a central role in this paper, is that the stabilization term can be made arbitrarily small relative to the a posteriori error estimators upon increasing the stabilization parameter. Our AVEM concatenates two modules, GALERKIN and DATA. The former deals with piecewise constant data and is shown in [8] to be a contraction between consecutive iterates. The latter approximates general data by piecewise constants to a desired accuracy. AVEM is shown to be convergent and quasi-optimal, in terms of error decay versus degrees of freedom, for solutions and data belonging to appropriate approximation classes. Numerical experiments illustrate the interplay between these two modules! and prov ide computational evidence of optimality