A new MOX report entitled “Clustering Hierarchies via a Semi-Parametric Generalized Linear Mixed Model: a statistical significance-based approach” by Ragni, A.; Masci, C.; Ieva, F.; Paganoni, A. M. has appeared in the MOX Report Collection.
The report can be donwloaded at the following link:
https://www.mate.polimi.it/biblioteca/add/qmox/15/2023.pdf
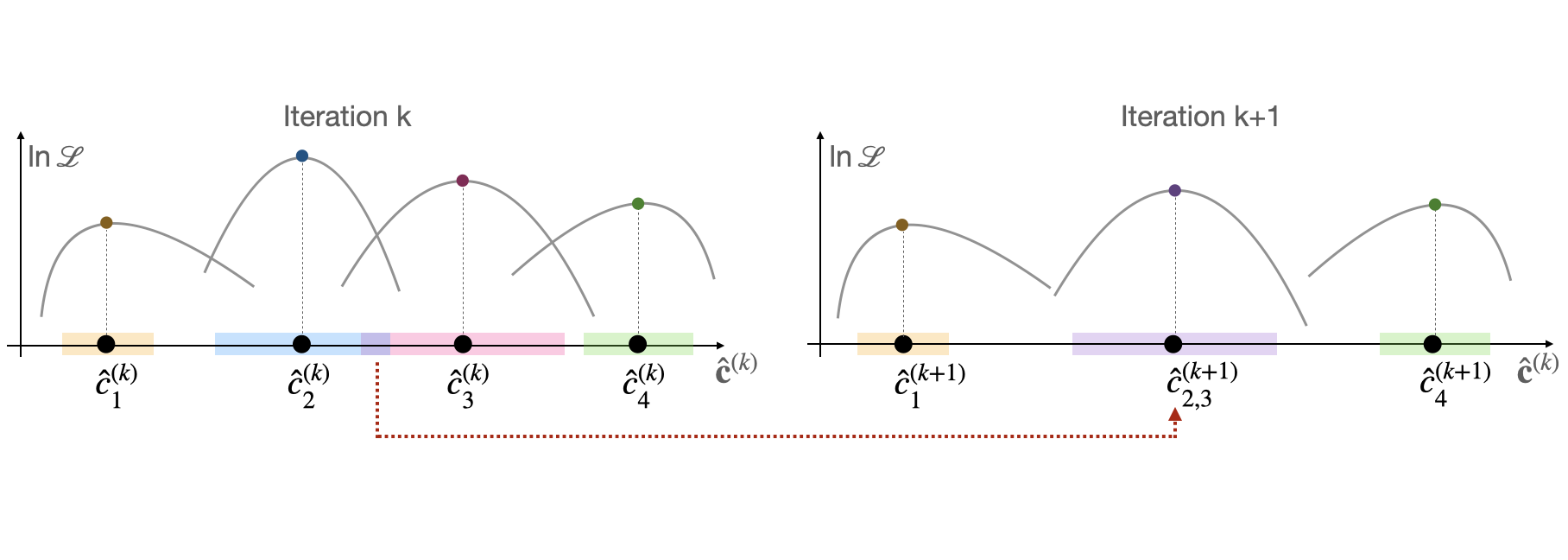
Abstract: We introduce a novel statistical significance-based approach for clustering hierarchical data using semi-parametric linear mixed-effects models designed for responses with laws in the exponential family (e.g., Poisson and Bernoulli). Within the family of semi-parametric mixed-effects models, a latent clustering structure of the highest-level units can be identified by assuming the random effects to follow a discrete distribution with an unknown number of support points. We achieve this by computing alpha-level confidence regions of the estimated support point and identifying statistically different clusters. At each iteration of a tailored Expectation Maximization algorithm, the two closest estimated support points for which the confidence regions overlap collapse. Unlike the related state-of-the-art methods that rely on arbitrary thresholds to determine the merging of close discrete masses, the proposed approach relies on conventional statisti! cal confi dence levels, thereby avoiding the use of discretionary tuning parameters. To demonstrate the effectiveness of our approach, we apply it to data from the Programme for International Student Assessment (PISA – OECD) to cluster countries based on the rate of innumeracy levels in schools. Additionally, a simulation study and comparison with classical parametric and state-of-the-art models are provided and discussed.