A new MOX report entitled “Discontinuous Galerkin Methods for Fisher-Kolmogorov Equation with Application to Alpha-Synuclein Spreading in Parkinson’s Disease” by Corti, M.; Antonietti, P.F.; Bonizzoni, F.; Dede’, L., Quarteroni, A. has appeared in the MOX Report Collection.
The report can be donwloaded at the following link:
https://www.mate.polimi.it/biblioteca/add/qmox/10/2023.pdf
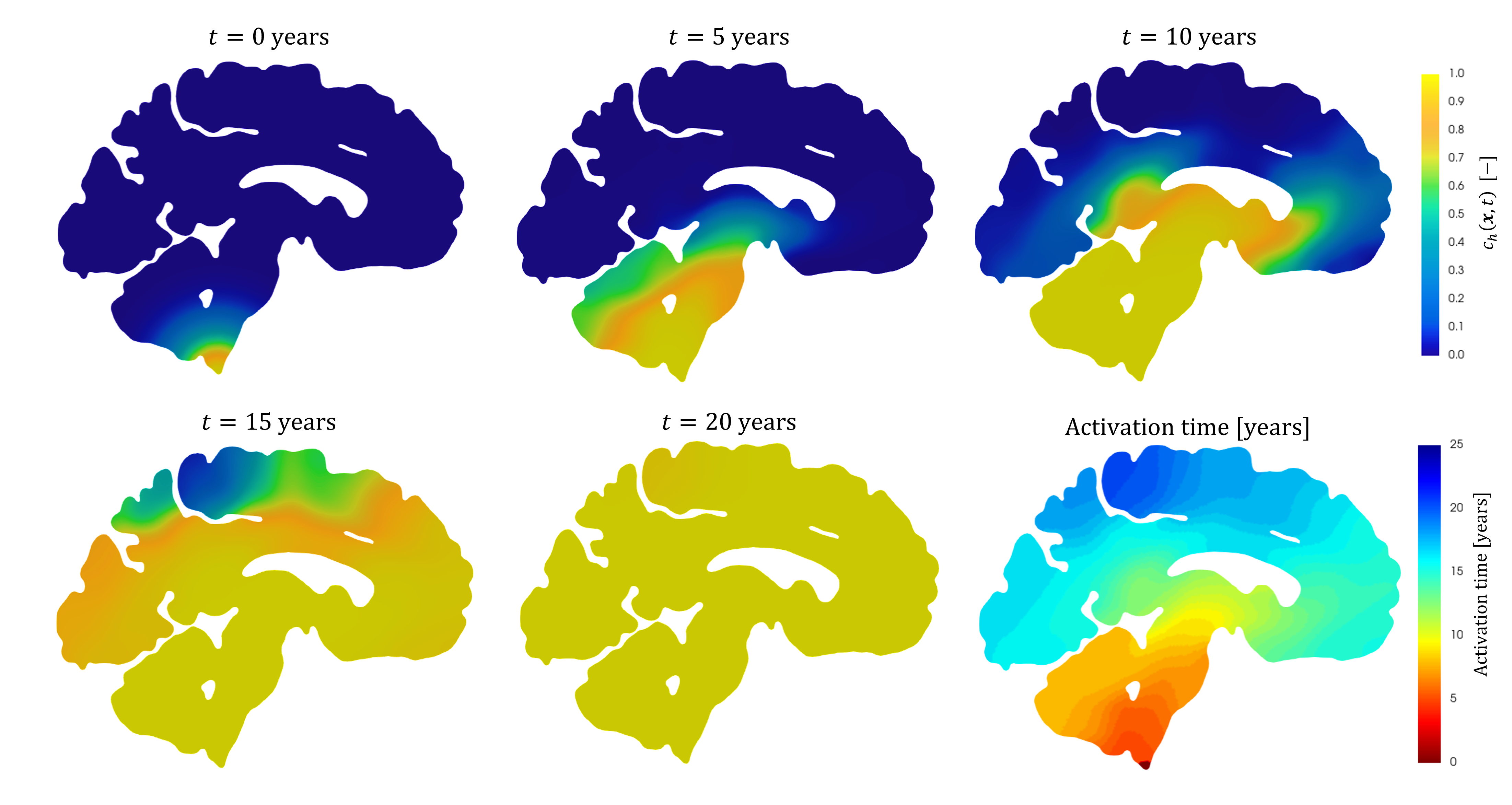
Abstract: The spreading of prion proteins is at the basis of brain neurodegeneration. The paper deals with the numerical modelling of the misfolding process of alpha-synuclein in Parkinson’s disease. We introduce and analyze a discontinuous Galerkin method for the semi-discrete approximation of the Fisher-Kolmogorov (FK) equation that can be employed to model the process. We employ a discontinuous Galerkin method on polygonal and polyhedral grids (PolyDG) for space discretization, which allows us to accurately simulate the wavefronts typically observed in the prionic spreading. We prove stability and a priori error estimates for the semi-discrete formulation. Next, we use a Crank-Nicolson scheme to advance in time. For the numerical verification of our numerical model, we first consider a manufactured solution, and then we consider a case with wavefront propagation in two-dimensional polygonal grids. Next, we carry out a simulation of alpha-synuclein s! preading in a two-dimensional brain slice in the sagittal plane with a polygonal agglomerated grid that takes full advantage of the flexibility of PolyDG approximation. Finally, we present a simulation in a three-dimensional patient-specific brain geometry reconstructed from magnetic resonance images.