A new MOX report entitled “Integrated Depths for Partially Observed Functional Data” by Elías, A.; Jiménez, R.; Paganoni, A.M.; Sangalli, L.M. has appeared in the MOX Report Collection.
The report can be donwloaded at the following link:
https://www.mate.polimi.it/biblioteca/add/qmox/50/2022.pdf
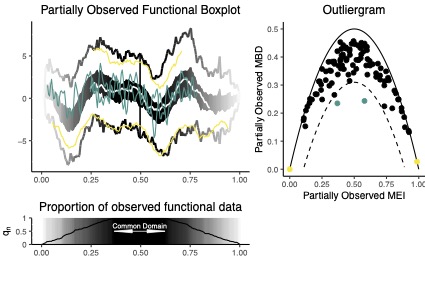
Abstract: Partially observed functional data are frequently encountered in applications and are the object of an increasing interest by the literature. We here address the problem of measuring the centrality of a datum in a partially observed functional sample. We propose an integrated functional depth for partially observed functional data, dealing with the very challenging case where partial observability can occur systematically on any observation of the functional dataset. In particular, differently f rom m any techniques f or partially observed functional data, we do not request that some functional datum is fully observed, nor we require that a common domain exist, where all of the functional data are recorded. Because of this, our proposal can also be used in those frequent situations where reconstructions methods and other techniques for partially observed functional data are inapplicable. By means of simulation studies, we demonstrate the very g! ood perfo rmances the proposed depth on finite samples. Our proposal enables the use of benchmark methods based on depths, originally introduced for fully observed data, in the case of partially observed functional data. This include the functional boxplot, the outliergram and the depth vs depth classifiers. We illustrate our proposal on two case studies, the first concerning a problem of outlier detection in German electricity supply functions, the second regarding a classification problem with data obtained from medical imaging.