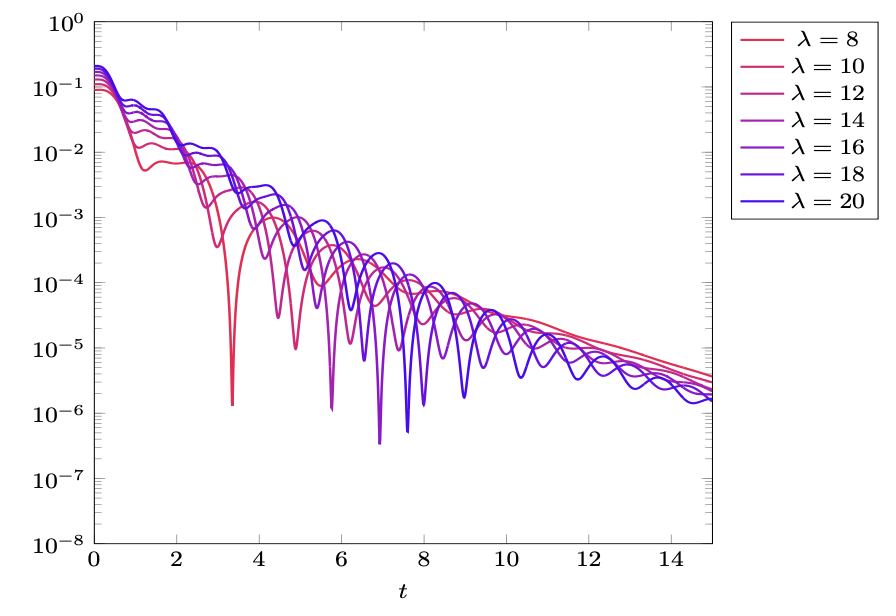
A new MOX report entitled “Lack of superstable trajectories in linear viscoelasticity: A numerical approach” by Antonietti, P.F.; Liverani, L.; Pata, V. has appeared in the MOX Report Collection.
The report can be donwloaded at the following link:
https://www.mate.polimi.it/biblioteca/add/qmox/66/2022.pdf
Abstract: Given a positive operator $A$ on some Hilbert space, and a nonnegative decreasing summable function $\mu$, we consider the abstract equation with memory $$ \ddot u(t)+ A u(t)- \int_0^t \mu(s)Au(t-s) ds=0 $$ modeling the dynamics of linearly viscoelastic solids. The purpose of this work is to provide numerical evidence of the fact that the energy $$E(t)=\Big(1-\int_0^t\mu(s)ds\Big)\|u(t)\|^2_1+\|\dot u(t)\|^2 +\int_0^t\mu(s)\|u(t)-u(t-s)\|^2_1ds,$$ of any nontrivial solution cannot decay faster than exponential, no matter how fast might be the decay of the memory kernel $\mu$. This will be accomplished by simulating the integro-differential equation for different choices of the memory kernel $\mu$ and of the initial data.