A new MOX report entitled “Numerical Modelling of the Brain Poromechanics by High-Order Discontinuous Galerkin Methods” by Corti, M.; Antonietti, P.F.; Dede’, L.; Quarteroni, A. has appeared in the MOX Report Collection.
The report can be donwloaded at the following link:
https://www.mate.polimi.it/biblioteca/add/qmox/63/2022.pdf
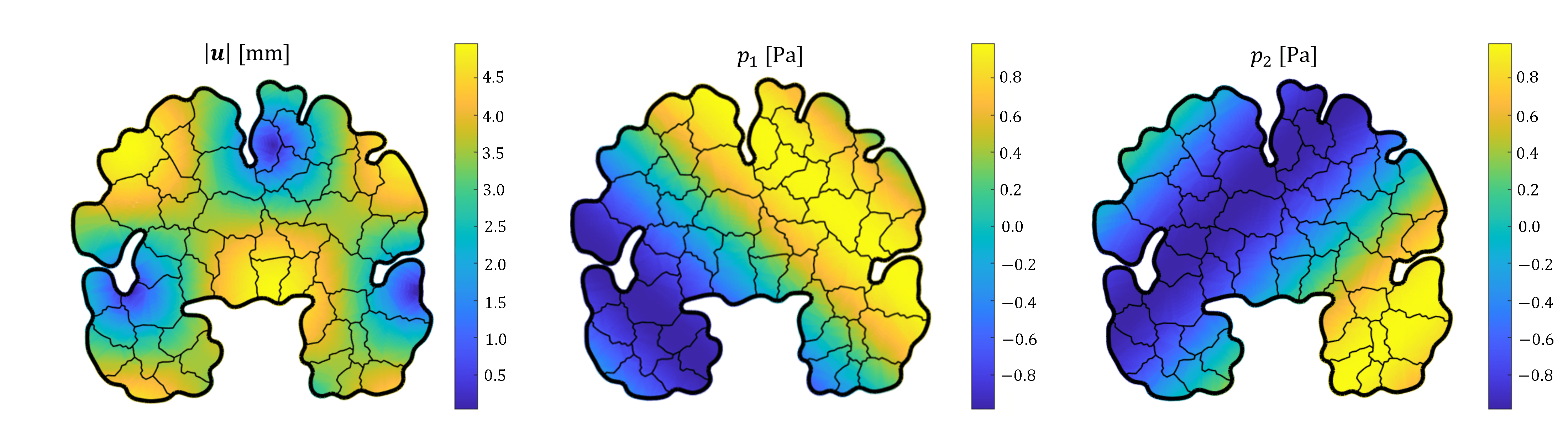
Abstract: We introduce and analyze a discontinuous Galerkin method for the numerical modelling of the equations of Multiple-Network Poroelastic Theory (MPET) in the dynamic formulation. The MPET model can comprehensively describe functional changes in the brain considering multiple scales of fluids. Concerning the spatial discretization, we employ a high-order discontinuous Galerkin method on polygonal and polyhedral grids and we derive stability and a priori error estimates. The temporal discretization is based on a coupling between a Newmark $\beta$-method for the momentum equation and a $\theta$-method for the pressure equations. After the presentation of some verification numerical tests, we perform a convergence analysis using an agglomerated mesh of a geometry of a brain slice. Finally we present a simulation in a three dimensional patient-specific brain reconstructed from magnetic resonance images. The model presented in this paper can be regarded! as a pre liminary attempt to model the perfusion in the brain.